Will The Neurotic Basketball Player Make His Next Free Throw? Problem
My proposed solution to FiveThirtyEight’s “The Riddler”, posted on January 15, 2016.
Problem
From: http://fivethirtyeight.com/features/will-the-neurotic-basketball-player-make-his-next-free-throw/
A basketball player is in the gym practicing free throws. He makes his first shot, then misses his second. This player tends to get inside his own head a little bit, so this isn’t good news. Specifically, the probability he hits any subsequent shot is equal to the overall percentage of shots that he’s made thus far. (His neuroses are very exacting.) His coach, who knows his psychological tendency and saw the first two shots, leaves the gym and doesn’t see the next 96 shots. The coach returns, and sees the player make shot No. 99. What is the probability, from the coach’s point of view, that he makes shot No. 100?
If we let $0$ denote the event of a missed shot, $1$ denote the event of a made shot, and $s_n$ denote the result of shot $n$, we are attempting to find $Pr(s_{100} = 1 \mid s_1 = 1, s_2 = 0, s_{99} = 1 $).
Simulation Solution
import random
from IPython.display import Image
# Create a function that can be used to obtain a possible sequence of shots
def rand_seq(shot):
x=[1,0]
for shot in range(3,shot):
probability = float(float(sum(x))/float(len(x)))
if random.random() < probability:
x.append(1)
else:
x.append(0)
return x
# Create a function that uses rand_seq function to obtain
# random sequences of 99 shots with shot_99 = 1 and find
# average probability shot_100 = 1 in the sequences
def prob_shot_100():
i=0
probabilities=[]
while i < 50000:
sequence = rand_seq(98)
prob_99 = float(float(sum(sequence))/float(len(sequence)))
if random.random() < prob_99:
sequence.append(1)
probabilities.append(float(float(sum(sequence))/float(len(sequence))))
i+=1
average_prob = float(float(sum(probabilities))/float(len(probabilities)))
print("The probability that he makes shot 100 is", average_prob, "!")
prob_shot_100()
The probability that he makes shot 100 is 0.6654732653061324 !
Proposed Proof and Intuition
First note that after the first two shots, our best guess of the player’s true probability of making a shot is $\frac{1}{2}$. In other words, given the first two shot results and no additional information, \(\begin{align*} Pr(s_n = 1 \mid s_1 = 1, s_2 = 0, n > 2) = 1/2. \end{align*}\) A formal proof of this as follows, \(\begin{align*} Pr(s_n = 1 \mid s_1 = 1, s_2 = 0, n > 2) &= \sum_{i=1}^{n-2} {n-3 \choose i-1} \frac{(i-1)!(n-i-2)!}{(n-2)!}\frac{i}{n-1} \\ &= \sum_{i=1}^{n-2} \frac{(n-3)!}{(i-1)!(n-i-2)!} \frac{(i-1)!(n-i-2)!}{(n-2)!}\frac{i}{n-1} \\ &= \frac{1}{(n-2)(n-1)}\sum_{i=1}^{n-2} i \\ &= \frac{(n-2)(n-1)}{2(n-2)(n-1)} \\ &= 1/2. \end{align*}\)
The formula used in the above proof has a nice interpretation. Given that the player has taken $n-1$ shots, we know that he must have made at least $1$ shot and no more than $n-2$ shots. This is why the summation runs from $1$ to $n-2$. If we know that the player has made $i$ shots and that he made the first shot and missed the second, we must choose the spots of the remaining $i-1$ makes from $n-3$ positions (i.e., ${n-3 \choose i-1}$). If the player has made $i$ shots in $n-1$ attempts, then his probability of making shot $n$ is certainly $\frac{i}{n-1}$. The $\frac{(i-1)!(n-i-2)!}{(n-2)!}$ term is best explained using an example.
Suppose we are interested in $Pr(s_7 = 1 \mid s_1 = 1, s_2 = 0, \sum_{i=1}^{6} = 3)$. One possible sequence of results, i.e., ($s_1, \dots, s_6)$, is $(1,0,0,1,1,0)$, which happens with probability, \(\begin{align*} \frac{1}{2}\times\frac{1}{3}\times\frac{2}{4}\times\frac{2}{5} &= \frac{2!2!}{5!} \\ &= \frac{(i-1)!(n-i-2)!}{(n-2)!} \end{align*}\)
We will use the fact that $Pr(s_n = 1 \mid s_1 = 1, s_2 = 0, n > 2) = 1/2$ below.
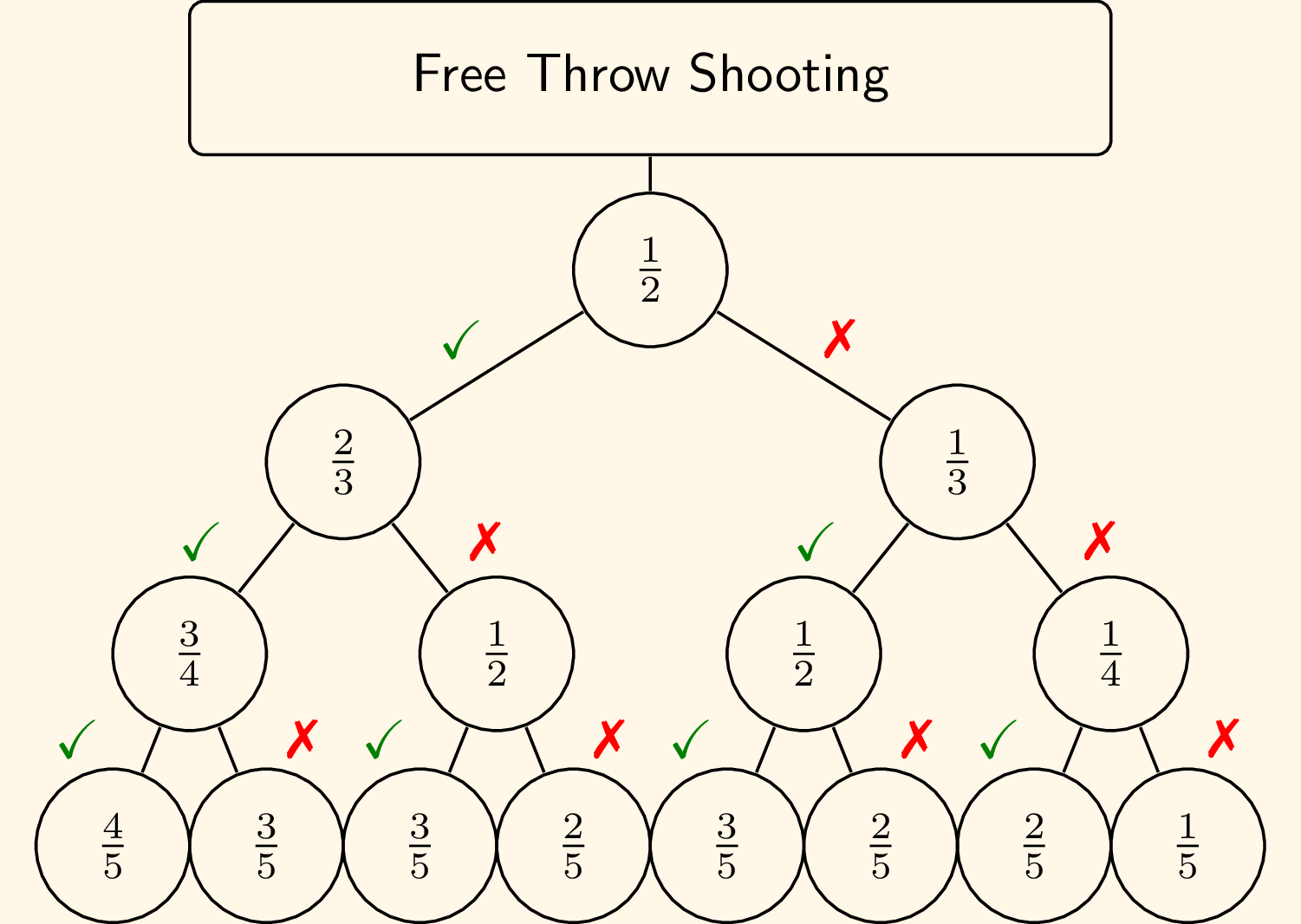
Back to the main problem, regardless of the shot number, whenever the coach comes back and sees a shot go in, the probability of the next shot going in, from the coach’s perspective, is $2/3$. Consider the diagram below. Given $s_1 = 1$ and $s_2 = 0$, if the coach sees the player make shot $3$, then $Pr(s_4 = 1)$ is trivially $2/3$.
If the coach came back and saw the player make shot $4$ (without any knowledge of shot $3$), then, \(\begin{align*} Pr(s_5 = 1 \mid s_1=1, s_2=0, s_4 = 1) &= \frac{Pr(s_3 = 1 \cap s_4 = 1)\times \frac{3}{4} + Pr(s_3 = 0 \cap s_4 = 1)\times \frac{1}{2}}{Pr(s_4 = 1)} \\ & = \frac{(\frac{1}{2}\times\frac{2}{3}\times\frac{3}{4} + \frac{1}{2}\times\frac{1}{3}\times\frac{2}{4})}{\frac{1}{2}} \\ & = 2/3. \end{align*}\) If the coach came back and saw the player make shot $5$ (without any knowledge of shots $3$ and $4$), then, \(\begin{align*} Pr(s_6 = 1 \mid s_1=1, s_2=0, s_5 = 1) &= \frac{Pr(s_3 = 1 \cap s_4 = 1 \cap s_5 = 1)\times \frac{4}{5} + \dots + Pr(s_3 = 0 \cap s_4 = 0 \cap s_5 = 1)\times \frac{2}{5}}{Pr(s_5 = 1)} \\ &= \frac{(\frac{1}{2}\times\frac{2}{3}\times\frac{3}{4}\times\frac{4}{5} + \dots + \frac{1}{2}\times\frac{2}{3}\times\frac{1}{4}\times\frac{2}{5})}{\frac{1}{2}} \\ &= 2/3. \end{align*}\)
We can generalize the above formulas: \(\begin{align*} Pr(s_n = 1 \mid s_1 = 1, s_2 = 0, s_{n-1} = 1, n > 2) &= \frac{\sum_{i=2}^{n-2} \frac{i}{n-1} {n-4 \choose i-2} \frac{(i-1)!(n-i-2)!}{(n-2)!}}{\frac{1}{2}} \\ &= 2\sum_{i=2}^{n-2} \frac{i}{n-1} \frac{(n-4)!}{(i-2)!(n-i-2)!} \frac{(i-1)!(n-i-2)!}{(n-2)!} \\ &= 2\sum_{i=2}^{n-2} \frac{i}{n-1} \frac{(n-4)!}{(i-2)!} \frac{(i-1)!}{(n-2)!} \\ &= 2\sum_{i=2}^{n-2} \frac{i(i-1)}{(n-1)(n-2)(n-3)} \\ &= \frac{2}{(n-1)(n-2)(n-3)}\sum_{i=2}^{n-2} i(i-1) \\ &= \frac{2}{(n-1)(n-2)(n-3)}\sum_{i=1}^{n-3} (i^2 + i) \\ &= \frac{2}{(n-1)(n-2)(n-3)}\Big(\frac{(n-3)(n-2)(2n-5)}{6} +\frac{(n-3)(n-2)}{2}\Big) \\ &= \frac{2}{(n-1)(n-2)(n-3)}\Big(\frac{(n-3)(n-2)(2n-2)}{6}\Big) \\ &= \frac{4n-4}{6n-6} \\ &= 2/3 \end{align*}\)
Again, the formula has an intuitive interpretation. The $\frac{i}{n-1}$ term, which can range from $\frac{2}{n-1}$ to $\frac{n-2}{n-1}$, represents each possible fraction of shots made so far. In other words, all we know is that the player made at least two shots (shot $1$ and shot $n-1$) and missed at least one shot (shot $2$). The ${n-4 \choose i-2}$ term represents the number of ways the player could have made $i$ shots in $n-1$ attempts. We know he made shot $1$, missed shot $2$, and made shot $n-1$, leaving $n-4$ shots to consider and $i-2$ makes to consider. The $\frac{(i-1)!(n-i-2)!}{(n-2)!}$ is again best understood through an illustration.
Suppose we are interested in $Pr(s_8 = 1 \mid s_1 = 1, s_2 = 0, s_7=1, \sum_{i=1}^{7} = 4)$. One possible sequence of results, i.e., ($s_1, \dots, s_7)$, is $(1,0,1,0,1,0,1)$, which happens with probability, \(\begin{align*} \frac{1}{2}\times\frac{1}{3}\times\frac{2}{4}\times\frac{2}{5}\times\frac{3}{6} &= \frac{3!2!}{6!} \\ &= \frac{(i-1)!(n-i-2)!}{(n-2)!}. \end{align*}\)
Finally, we divide by $\frac{1}{2}$ since we are conditioning on $s_{n-1} = 1$.