Monte Carlo Estimation of Pi
Yesterday, I came across a neat way to approximate π using Monte Carlo simulation. I hadn’t seen this exercise before, but I think it is understandable and illustrative, so I decided to give it a try using both Excel and Python.
How it Works
Imagine we have a unit circle inscribed within a 2x2 square.
%matplotlib inline
import matplotlib.pyplot as plt
plt.xlim(xmin=-1)
plt.ylim(ymin=-1)
circle1=plt.Circle((0,0),1,color='MidnightBlue')
fig = plt.gcf()
fig.gca().add_artist(circle1)
fig.set_size_inches(5, 5)
Now, let’s zoom into the top-right quadrant of this plot.
circle2=plt.Circle((0,0),1,color='MidnightBlue')
fig = plt.gcf()
fig.gca().add_artist(circle2)
fig.set_size_inches(5, 5)
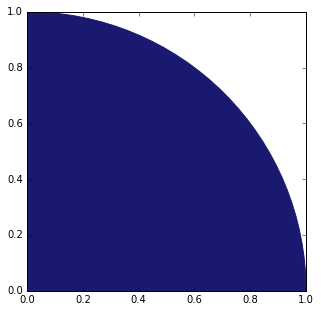
The area of this entire quadrant is equal to r2 (since the base of the square equals the circle’s radius). The area in blue is a quarter-circle and is equal to (1/4)πr2. Thus, if one were to plot points within this quadrant at random, we would expect that π/4 (approximately 78.54%) would lie within the blue region. Theoretically, then, to estimate π, one can generate a bunch of coordinate pairs with x and y values between 0 and 1. If the distance of a particular point from the origin is greater than 1 (greater than the radius of the circle), it is classified as outside of the circle. Otherwise, it is contained within the circle. With a large enough sample, the proportion of points within the circle should be close to π/4. We can then multiply this proportion by 4 to estimate π.
To get the distance of a point from the origin, we use the Pythagorean theorem:
Distance=$\sqrt{x^{2} + y^{2}}$.
Executing this using Excel
To carry out this process in Excel, I created two separate sets of
11,175 random numbers between 0 and 1 using the =RAND() function. I then
calculated the distance for each pair. Next, I used an =IF() function to
generate indicator variables corresponding to whether or not the
calculated distance was greater than 1. Finally, I used =COUNTIF() to
count those distances less than or equal to 1, divided this count by the
total number of distances calculated (11,175), and multiplied this
fraction by 4 to get an estimate of π.
Once all of this is in place, it is quick and easy to get estimates by
pressing F9 to refresh the random numbers.
Here are 10 of the estimates I generated (accurate to 5 digits):
3.14917, 3.12447, 3.14309, 3.13879, 3.14452, 3.14130, 3.12197, 3.12841, 3.13128, 3.15347
For reference, the true value of π to 5 digits is 3.14159.
Here is a spreadsheet setup to carry out this simulation exercise.
Executing this using Python
Using 100,000 random number pairs, here are 10 estimates that I got:
#single point estimate
import random
from math import *
from __future__ import division
i=0
for i in range(10):
n=100000 #number of random number pairs
my_randoms = [] #create empty list to store distance calculations
for _ in range(0,n):
my_randoms.append(sqrt((random.random()**2) + (random.random()**2))) #distance calculation
pi_estimate=(sum(x<=1 for x in my_randoms)/n)*4
print(pi_estimate,)
i+=1
3.13704
3.1436
3.13956
3.14492
3.13784
3.1414
3.14296
3.13688
3.144
3.146
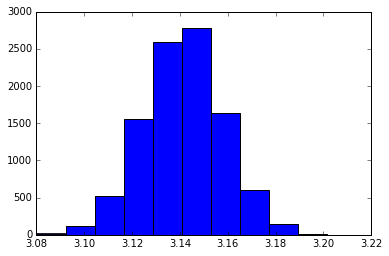
Simulating this process programatically also allowed me to go one step further. Again, I used the random number pairs to generate an estimate of π (this time “only” 10,000 pairs to spare my computer from the extra calculations). However, using a nested for-loop, I repeated this process 10,000 times! One can then take the average of the 10,000 π estimates to get an even better approximation of π. Additionally, one can test the validity of the Central Limit Theorem to see if the 10,000 estimates are normally distributed.
Here’s my Python code to do just this:
# average of 10,000 estimates
import random
from math import *
from __future__ import division
import matplotlib.pyplot as plt
n1= 10000 # number of pi estimates
n2= 10000 # number of random number pairs to use in pi estimate
pi_list=[] # create empty list to store pi estimates
for _ in range(0,n1): # n1 iterations
my_randoms=[] # create empty list to store distance calculations
for _ in range(0,n2):
my_randoms.append(sqrt((random.random()**2) + (random.random()**2))) # distance calculation
pi_list.append((sum(x<=1 for x in my_randoms)/n2)*4)
print("Estimate:", sum(pi_list) / float(len(pi_list))) # average pi estimate
_ = plt.hist(pi_list) # histogram of pi estimates
Estimate: 3.141337599999959